什么是深度学习 ?
深度学习的历史可以追溯到 20 世纪 40 年代。深度学习看似是一个全新的领域,只不过因为在目前流行的前几 年它是相对冷门的,同时也因为它被赋予了许多不同的名称(其中大部分已经不再使用),最近才成为众所周知的 “深度学习’’。这个领域已经更换了很多名称,它反映了不同的研究人员和不同观点的影响。一般来说,目前为止深度学习已经经历了三次发展浪潮:20 世纪 40 年代到 60 年代深度学习的雏形出现在 控制论(cybernetics)中,20 世纪 80 年代 到 90 年代深度学习表现为 联结主义(connectionism),直到 2006 年,才真正以深度学习之名复兴。
现代术语 “深度学习’’ 超越了目前机器学习模型的神经科学观点。它诉诸于学 习多层次组合这一更普遍的原理,这一原理也可以应用于那些并非受神经科学启发的机器学习框架。 深度学习最大的用处是他可以学习非线性函数。最经典的一个机器学习的例子是一个简单的单层神经网络就可以学习到XOR函数。现在,神经科学被视为深度学习研究的一个重要灵感来源,但它已不再是该领域的主要指导。
如今神经科学在深度学习研究中的作用被削弱,主要原因是我们根本没有足够 的关于大脑的信息来作为指导去使用它。要获得对被大脑实际使用算法的深刻理解,我们需要有能力同时监测(至少是)数千相连神经元的活动。我们不能够做到这一点,所以我们甚至连大脑最简单、最深入研究的部分都还远远没有理解。深度学习的另一个最大的成就是其在 强化学习(reinforcement learning)领域的扩展。在强化学习中,一个自主的智能体必须在没有人类操作者指导的情况下,通过试错来学习执行任务。DeepMind 表明,基于深度学习的强化学习系统能够学会玩 Atari 视频游戏,并在多种任务中可与人类匹敌 (Mnih et al., 2015)。深度学习也显著改善了机器人强化学习的性能 (Finn et al., 2015)。
总之,深度学习是机器学习的一种方法。在过去几十年的发展中,它大量借鉴了我们关于人脑、统计学和应用数学的知识。近年来,得益于更强大的计算机、更大的数据集和能够训练更深网络的技术,深度学习的普及性和实用性都有了极大的发展。未来几年充满了进一步提高深度学习并将它带到新领域的挑战和机遇。
深度学习的流程
一项机器学习任务时常常有以下的几个重要步骤,首先是数据的预处理,其中重要的步骤包括数据格式的统一、异常数据的消除和必要的数据变换,同时划分训练集、验证集、测试集,常见的方法包括:按比例随机选取,KFold方法(我们可以使用sklearn带的test_train_split函数、kfold来实现)。接下来选择模型,并设定损失函数和优化方法,以及对应的超参数(当然可以使用sklearn这样的机器学习库中模型自带的损失函数和优化器)。最后用模型去拟合训练集数据,并在验证集/测试集上计算模型表现。
深度学习和机器学习在流程上类似,但在代码实现上有较大的差异。首先,由于深度学习所需的样本量很大,一次加载全部数据运行可能会超出内存容量而无法实现;同时还有批(batch)训练等提高模型表现的策略,需要每次训练读取固定数量的样本送入模型中训练,因此深度学习在数据加载上需要有专门的设计。在模型实现上,深度学习和机器学习也有很大差异。由于深度神经网络层数往往较多,同时会有一些用于实现特定功能的层(如卷积层、池化层、批正则化层、LSTM层等),因此深度神经网络往往需要“逐层”搭建,或者预先定义好可以实现特定功能的模块,再把这些模块组装起来。这种“定制化”的模型构建方式能够充分保证模型的灵活性,也对代码实现提出了新的要求。
深度学习中训练和验证过程最大的特点在于读入数据是按批的,每次读入一个批次的数据,放入GPU中训练,然后将损失函数反向传播回网络最前面的层,同时使用优化器调整网络参数。这里会涉及到各个模块配合的问题。训练/验证后还需要根据设定好的指标计算模型表现。
神经网络结构
抽象点讲神经网络是由无数个神经元组成的. 真实点讲的话,就是神经网络是由无数线性函数外套非线性函数组成的. 一般我们叫这一层非线性函数为: 激活函数(Activation Function).
常见的激活函数
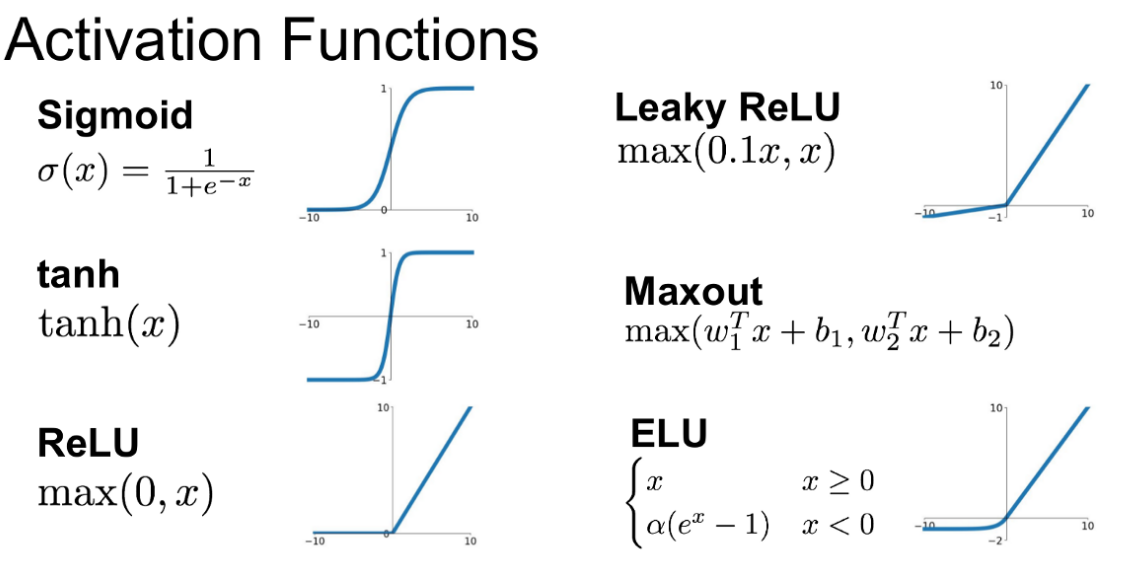
Sigmoid
sigmoid是使用范围最广的一类激活函数,具有指数的形状,它在物理意义上最为接近神经元。sigmoid的输出是(0,1),具有很好的性质,可以被表示做概率或者用于输入的归一化等等。
然而,sigmoid也具有自身的缺陷。第一点,最明显的就是饱和性,从上图也不难看出其两侧导数逐渐趋近于0,
即
第二点,激活函数的偏移现象。sigmoid函数的输出值均大于0,使得输出不是0的均值,这会导致后一层的神经元将得到上一层非0均值的信号作为输入。
Tanh
tanh也是一种非常常见的激活函数,与sigmoid相比,它的输出均值为0,这使得它的收敛速度要比sigmoid快,减少了迭代更新的次数。
然而tanh和sigmoid一样具有饱和性,会造成梯度消失。
Rectified Linear Units (ReLU)
ReLU是针对sigmoid和tanh的饱和性二提出的新的激活函数。从上图中可以很容易的看到,当
然而,随着训练的推进,部分输入会落入硬饱和区(即
而且,与sigmoid类似,ReLU的输出均值也大于0,偏移现象和神经元死亡会共同影响网络的收敛性。
SoftPlus
SoftPlus可以作为ReLu的一个不错的替代选择,可以看到与ReLU不同的是,SoftPlus的导数是连续的、非零的、无处不在的,这一特性可以防止出现ReLU中的“神经元死亡”现象。
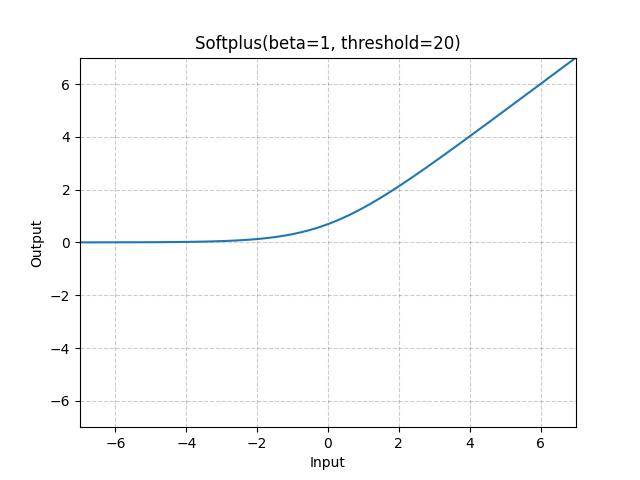
然而,SoftPlus是不对称的,不以0为中心,存在偏移现象;而且,由于其导数常常小于1,也可能会出现梯度消失的问题。
SoftMax
Softmax 一般用作输出层, 主要针对分类问题. Softmax 会计算各个种类的概率,而且会normalize 输出使其输出的总和(总概率)为 1. 因此,Softmax 层的节点数必须与输出层的节点数相同。

Maxout
可以注意到,ReLU 和 Leaky-ReLU 都是它的一个变形。这个激活函数有点大一统的感觉,因为maxout网络能够近似任意连续函数,且当 为0时,退化为ReLU。Maxout能够缓解梯度消失,同时又规避了ReLU神经元死亡的缺点,但增加了参数和计算量。
常见的损失函数
Cross-Entropy
Cross-Entropy 本质上也是一种对数似然函数,可用于二分类和多分类任务中。
MDE
Hinge 损失函数
hinge损失函数表示如果被分类正确,损失为0,否则损失就为
深度学习经典实例:神经网络学习 XOR 算法
XOR 函数("异或" 逻辑)是两个二进制值 x1 和
x2 的运算。当这些二进制值 中恰好有一个为 1 时,XOR
函数返回值为 1。其余情况下返回值为 0。XOR
函数提供了我们想要学习的目标函数 θ 来使得
f 尽可能接近
在这个简单的例子中, 统计泛化并不重要。首先我们可以把这个问题当作是回归问题,并使用均方误差损失函数。我们选择这 个损失函数是为了尽可能简化本例中用到的数学。在应用领域,对于二进制数据建模时,MSE通常并不是一个合适的损失函数。
假设这是一个线性模型,损失函数我们用MSE,模型的目标函数是
如果我们在此基础上加入一个隐藏层,这个隐藏层的激活函数我们用RELU(rectified
linear unit)。这个模型就变成了
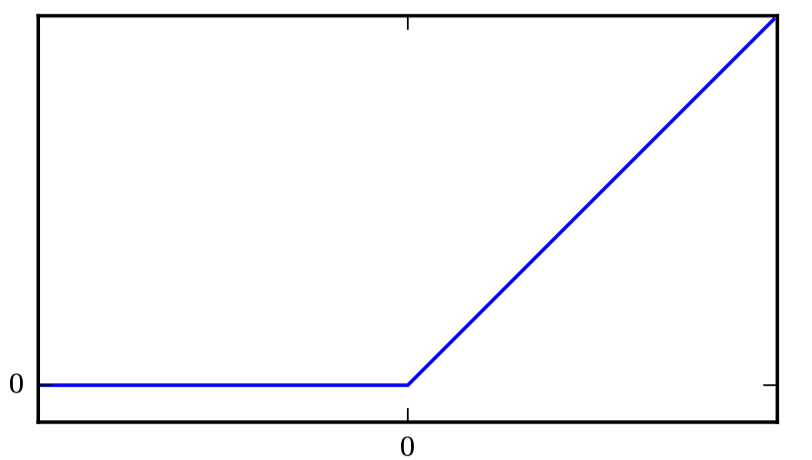
神经网络对这XOR函数的每个样本都给出了正确的结果。在这个例子中,我们简单地指定了解决方案,然后说明它得到的误差为零。在实际情况中,可能会有数十亿的模型参数以及数十亿的训练样本,所以不能像我们这里做的那样进行简单地猜解。与之相对的,基于梯度的优化算法可以找到一些参数使得产生的误差非常小。我们这里给出的 XOR 问题的解处在损失函数的全局最小点,所以梯度下降算法可以收敛到这一点。梯度下降算法还可以找到 XOR 问题一些其他的等价解。梯度下降算法的收敛点取决于参数的初始值。在实践中,梯度下降通常不会找到像我们这里给出的那种干净的、容易理解的、整数值的解。